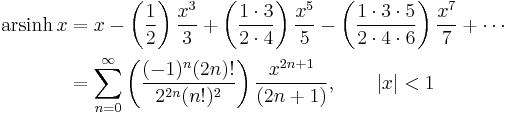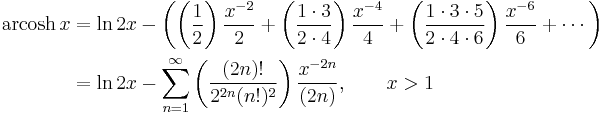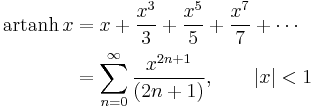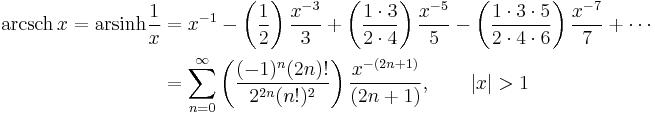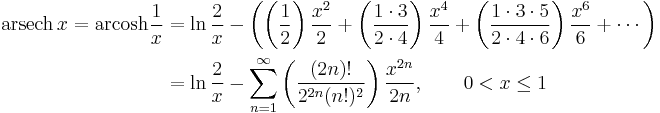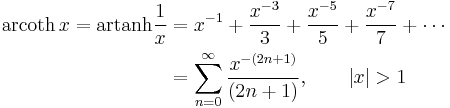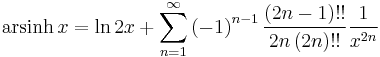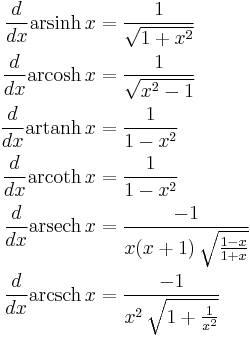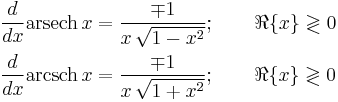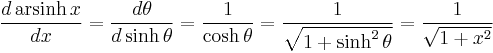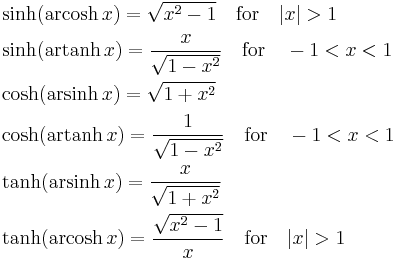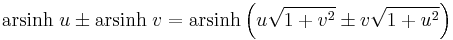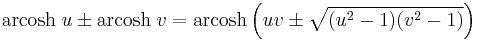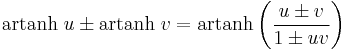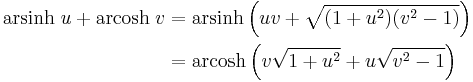Inverse hyperbolic function

The inverses of the hyperbolic functions are the area hyperbolic functions. The names hint at the fact that they give the area of a sector of the unit hyperbola x2 − y2 = 1 in the same way that the inverse trigonometric functions give the arc length of a sector on the unit circle x2 + y2 = 1. The abbreviations arcsinh, arccosh, etc., are commonly used, even though they are misnomers, since the prefix arc is the abbreviation for arcus, while the prefix ar stands for area.[1][2][3]Other authors prefer to use the notation argsinh, argcosh, argtanh, and so on. In computer science this is often shortened to asinh. The notation sinh−1(x), cosh−1(x), etc., is also used, despite the fact that care must be taken to avoid misinterpretations of the superscript −1 as a power as opposed to a shorthand for inverse (e.g., cosh−1(x) versus cosh(x)−1).

The values of inverse hyperbolic functions are hyperbolic angles.

Contents

Logarithmic representation

The operators are defined in the complex plane by:

\begin{align} \operatorname{arsinh}\, z &= \ln(z %2B \sqrt{z^2 %2B 1} \,), \\[2.5ex] \operatorname{arcosh}\, z &= \ln(z %2B \sqrt{z%2B1} \sqrt{z-1} \,), \\[1.5ex] \operatorname{artanh}\, z &= \tfrac12\ln\frac{1%2Bz}{1-z}, \\ \operatorname{arcoth}\, z &= \tfrac12\ln\frac{z%2B1}{z-1}. \\ \operatorname{arcsch}\, z &= \ln\left( \frac{1}{z} %2B \sqrt{ \frac{1}{z^2} %2B1 } \,\right), \\ \operatorname{arsech}\, z &= \ln\left( \frac{1}{z} %2B \sqrt{ \frac{1}{z} %2B 1 } \, \sqrt{ \frac{1}{z} -1 } \,\right). \end{align}

The above square roots are principal square roots, and the logarithm function is the complex logarithm. For real arguments, i.e., z = x, which return real values, certain simplifications can be made e.g. 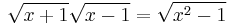\sqrt{x%2B1}\sqrt{x-1}=\sqrt{x^2-1}, which are not generally true when using principal square roots.

Inverse hyperbolic functions in the complex plane
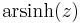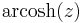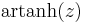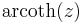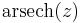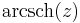\operatorname{arsinh}(z) \operatorname{arcosh}(z) \operatorname{artanh}(z) \operatorname{arcoth}(z) \operatorname{arsech}(z) \operatorname{arcsch}(z)

Series expansions

Expansion series can be obtained for the above functions:

\begin{align}\operatorname{arsinh}\, x & = x - \left( \frac {1} {2} \right) \frac {x^3} {3} %2B \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^5} {5} - \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^7} {7} %2B\cdots \\ & = \sum_{n=0}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{2n%2B1}} {(2n%2B1)} , \qquad \left| x \right| < 1 \end{align}
\begin{align}\operatorname{arcosh}\, x & = \ln 2x - \left( \left( \frac {1} {2} \right) \frac {x^{-2}} {2} %2B \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{-4}} {4} %2B \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{-6}} {6} %2B\cdots \right) \\ & = \ln 2x - \sum_{n=1}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{-2n}} {(2n)} , \qquad x > 1 \end{align}
\begin{align}\operatorname{artanh}\, x & = x %2B \frac {x^3} {3} %2B \frac {x^5} {5} %2B \frac {x^7} {7} %2B\cdots \\ & = \sum_{n=0}^\infty \frac {x^{2n%2B1}} {(2n%2B1)} , \qquad \left| x \right| < 1 \end{align}
\begin{align}\operatorname{arcsch}\, x = \operatorname{arsinh} \frac1x & = x^{-1} - \left( \frac {1} {2} \right) \frac {x^{-3}} {3} %2B \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{-5}} {5} - \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{-7}} {7} %2B\cdots \\ & = \sum_{n=0}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{-(2n%2B1)}} {(2n%2B1)} , \qquad \left| x \right| > 1 \end{align}
\begin{align}\operatorname{arsech}\, x = \operatorname{arcosh} \frac1x & = \ln \frac{2}{x} - \left( \left( \frac {1} {2} \right) \frac {x^{2}} {2} %2B \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{4}} {4} %2B \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{6}} {6} %2B\cdots \right) \\ & = \ln \frac{2}{x} - \sum_{n=1}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{2n}} {2n} , \qquad 0 < x \le 1 \end{align}
\begin{align}\operatorname{arcoth}\, x = \operatorname{artanh} \frac1x & = x^{-1} %2B \frac {x^{-3}} {3} %2B \frac {x^{-5}} {5} %2B \frac {x^{-7}} {7} %2B\cdots \\ & = \sum_{n=0}^\infty \frac {x^{-(2n%2B1)}} {(2n%2B1)} , \qquad \left| x \right| > 1 \end{align}

Asymptotic expansion for the arsinh x is given by

\operatorname{arsinh}\, x = \ln 2x %2B \sum\limits_{n = 1}^\infty {\left( { - 1} \right)^{n - 1} \frac{{\left( {2n - 1} \right)!!}}{{2n\left( {2n} \right)!!}}} \frac{1}{{x^{2n} }}

Derivatives

\begin{align} \frac{d}{dx} \operatorname{arsinh}\, x & {}= \frac{1}{\sqrt{1%2Bx^2}}\\ \frac{d}{dx} \operatorname{arcosh}\, x & {}= \frac{1}{\sqrt{x^2-1}}\\ \frac{d}{dx} \operatorname{artanh}\, x & {}= \frac{1}{1-x^2}\\ \frac{d}{dx} \operatorname{arcoth}\, x & {}= \frac{1}{1-x^2}\\ \frac{d}{dx} \operatorname{arsech}\, x & {}= \frac{-1}{x(x%2B1)\,\sqrt{\frac{1-x}{1%2Bx}}}\\ \frac{d}{dx} \operatorname{arcsch}\, x & {}= \frac{-1}{x^2\,\sqrt{1%2B\frac{1}{x^2}}}\\ \end{align}

For real x:

\begin{align} \frac{d}{dx} \operatorname{arsech}\, x & {}= \frac{\mp 1}{x\,\sqrt{1-x^2}}; \qquad \Re\{x\} \gtrless 0\\ \frac{d}{dx} \operatorname{arcsch}\, x & {}= \frac{\mp 1}{x\,\sqrt{1%2Bx^2}}; \qquad \Re\{x\} \gtrless 0 \end{align}

For an example differentiation: let θ = arsinh x, so:

\frac{d\,\operatorname{arsinh}\, x}{dx} = \frac{d \theta}{d \sinh \theta} = \frac{1} {\cosh \theta} = \frac{1} {\sqrt{1%2B\sinh^2 \theta}} = \frac{1}{\sqrt{1%2Bx^2}}

Composition of hyperbolic and inverse hyperbolic functions

\begin{align} &\operatorname{sinh}(\operatorname{arcosh}\,x) = \sqrt{x^{2} - 1} \quad \text{for} \quad |x| > 1 \\ &\operatorname{\sinh}(\operatorname{artanh}\,x) = \frac{x}{\sqrt{1-x^{2}}} \quad \text{for} \quad -1 < x < 1 \\ &\operatorname{\cosh}(\operatorname{arsinh}\,x) = \sqrt{1%2Bx^{2}} \\ &\operatorname{\cosh}(\operatorname{artanh}\,x) = \frac{1}{\sqrt{1-x^{2}}} \quad \text{for} \quad -1 < x < 1 \\ &\operatorname{\tanh}(\operatorname{arsinh}\,x) = \frac{x}{\sqrt{1%2Bx^{2}}} \\ &\operatorname{\tanh}(\operatorname{arcosh}\,x) = \frac{\sqrt{x^{2} - 1}}{x} \quad \text{for} \quad |x| > 1 \end{align}

Addition formulae

\operatorname{arsinh} \;u \pm \operatorname{arsinh} \;v = \operatorname{arsinh} \left(u \sqrt{1 %2B v^2} \pm v \sqrt{1 %2B u^2}\right)
\operatorname{arcosh} \;u \pm \operatorname{arcosh} \;v = \operatorname{arcosh} \left(u v \pm \sqrt{(u^2 - 1) (v^2 - 1)}\right)
\operatorname{artanh} \;u \pm \operatorname{artanh} \;v = \operatorname{artanh} \left( \frac{u \pm v}{1 \pm uv} \right)
\begin{align}\operatorname{arsinh} \;u %2B \operatorname{arcosh} \;v & = \operatorname{arsinh} \left(u v %2B \sqrt{(1 %2B u^2) (v^2 - 1)}\right) \\ & = \operatorname{arcosh} \left(v \sqrt{1 %2B u^2} %2B u \sqrt{v^2 - 1}\right) \end{align}

See also

References

  1. ^ As stated by Jan Gullberg, Mathematics: From the Birth of Numbers (New York: W. W. Norton & Company, 1997), ISBN 039304002X, p. 539:

    Another form of notation, arcsinh x, arccosh x, etc., is a practice to be condemned as these functions have nothing whatever to do with arc, but with area, as is demonstrated by their full Latin names,

    arsinh     area sinus hyperbolicus
    arcosh     area cosinus hyperbolicus, etc.

  2. ^ As stated by Eberhard Zeidler, Wolfgang Hackbusch and Hans Rudolf Schwarz, translated by Bruce Hunt, Oxford Users' Guide to Mathematics (Oxford: Oxford University Press, 2004), ISBN 0198507631, Section 0.2.13: "The inverse hyperbolic functions", p. 68: "The Latin names for the inverse hyperbolic functions are area sinus hyperbolicus, area cosinus hyperbolicus, area tangens hyperbolicus and area cotangens hyperbolicus (of x). ..." This aforesaid reference uses the notations arsinh, arcosh, artanh, and arcoth for the respective inverse hyperbolic functions.
  3. ^ As stated by Ilja N. Bronshtein, Konstantin A. Semendyayev, Gerhard Musiol and Heiner Muehlig, Handbook of Mathematics (Berlin: Springer-Verlag, 5th ed., 2007), ISBN 3540721215, doi:10.1007/978-3-540-72122-2, Section 2.10: "Area Functions", p. 91:

    The area functions are the inverse functions of the hyperbolic functions, i.e., the inverse hyperbolic functions. The functions sinh x, tanh x, and coth x are strictly monotone, so they have unique inverses without any restriction; the function cosh x has two monotonic intervals so we can consider two inverse functions. The name area refers to the fact that the geometric definition of the functions is the area of certain hyperbolic sectors ...

External links